Use of Bonferroni Multiple Testing Correction With an Internet Based Calculator. An Analysis of User Behaviour.

There is concern about possible inappropriate use of Bonferroni correction in medical and epidemiological research (1-7). In Bonferroni correction one lowers the p-value to consider the use of multiple tests to answer a research question and to thus prevent an inflated type one error, the hypothesis of no difference or "effect" being incorrectly rejected. This is because by looking at the data multiple times to answer a single question one increases the chance of finding a statistically significant result. Making a type one error could result in ineffective policies, medical treatments and social or technical innovations being adopted which could lead to social and financial costs. However, using Bonferroni correction often results in loss of power and an inflated error type two, resulting in important and relevant results not being spotted (4). This in turn might lead to new effective innovations and technologies incorrectly not being adopted and promising lines of research being abandoned.

Among the attractive aspects of the Bonferroni method is that it is simple to apply, it uses only the p-values and does not require other statistics, access to the source data or complicated calculations, and the procedure can be limited to exactly the number of tests considered to answer a research question. A problem is that Bonferroni adjustment can be very conservative, particularly when there is dependence between tests. There are a number of strategies to address this conservative nature of Bonferroni adjustment.

Dependence between tests occurs in two often observed situations (9). First, multiple group comparisons where k experimental groups are compared with a control group. When there is statistical significance between one of the experimental groups and the control group an "effect" is declared with the Bonferroni threshold being p/k. An assumption of Bonferroni adjustment is that the experimental groups are independent. That would, for example, not be the case if the experimental groups consider different variants of the same treatment (10). Second, the multiple outcome situation is when more than one outcome is measured on each study subject and an overall "effect" would be declared when there is a difference between subjects in one of the outcomes. To use Bonferroni correction with p divided by the number of outcomes would be conservative given the highly probable correlation between the outcomes at both the person and the group level (3).

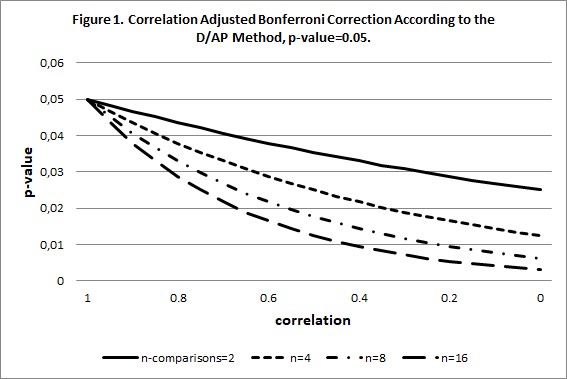
A correction for dependence in Bonferroni adjustment has been proposed by Dubey and Armitage-Parmar (D/AP method) (11), this correction is a generalization of an earlier procedure (10). With this D/AP method full Bonferroni correction is applied in the case that there is no dependence, and no Bonferroni correction is applied when there is complete dependence. How a correlation, as indicator of dependence, relates to a number of tests in Bonferroni correction according to the D/AP method is shown in figure one for a given p-value of 0.05 and different numbers of tests. In the top left of the figure, were all the curved lines come together, is the case of full correlation, and therefore no Bonferroni correction, on the right side, were the curved lines are most apart, the case of zero correlation, and full Bonferroni correction.

Another method to tackle the low power of the Bonferroni procedure is the Holm's stepwise procedure (12,13). The p-values are ordered from low to high and a decision is taken on each individual p-value step by step while recalculating the Bonferroni correction after each step. This procedure is considerably more powerful as the usual procedure where a single correction is applied for all p-values and is advised in preference above the standard Bonferroni method (14). The Holmes method also presumes independence between outcomes but the method can be combined with the D/AP method.

There are a number of articles which give advice on when (not) to apply Bonferroni correction (2,8). There is however so much discussion between scientists and practitioners about the Bonferroni procedure that it seems impossible to give a generally applicable advice. Another problem is that in publications which are accessible to practitioners the problem of dependence is rarely discussed with the result that correction for dependence is not often applied.

On the SISA website there is a form which enables the calculations for various Bonferroni procedures (15). The webpage has an option to consider correlation between the tests and the Holm's method. As the SISA website can log the use of its procedures it is possible to study to some extent how Bonferroni correction is used in practice. In this paper we will look at the pattern of Bonferroni correction, what p-value and number of multiple tests is given, if correlated Bonferroni analysis is requested, and about the use of the Holms procedure as an alternative to the classical Bonferroni correction.

Digital trace data are the data which is left behind by people as they engage in digital activities (16). As it often concerns very large data sets it allows for the use of novel analytical methods and is therefore seen as an important data source for the future (17). However, many questions with regard to the validity and the theoretical and practical capabilities of trace data are still to be explored (16). For example, as the user is unaware of being observed, or doesn't have a choice with regard to being observed, the data maybe suffers less from the biases of observer error, socially desirable answers, refusals and non-response (18). On the other hand, trace data is mostly unstructured, is not designed to answer specific research questions, a user profile by socio-demographic indicators is hard to obtain, and the user cannot be asked about motivations, attitudes and expected outcomes with regard to the activity which is being monitored (18). The analysis in this paper is an example of a trace data analysis to answer a question in relation as to how scientists use a statistical procedure. The analysis is basic because the website from which the data is sourced collects only limited information. The analysis presented concerns data which is logged when the user asks the website to calculate something. The main aim of this paper is then to provide an insight with regard to the use of Bonferroni correction "in the wild". Other research, for example a review of how the procedure is used in published papers, or a survey among researchers, can provide other insights (2,18). In the context of the analysis undertaken, some aspects of website trace data and possible methods of analysis and limitations are discussed.

METHODS

The data concerns the use of the SISA Bonferroni procedure on the SISA website for the year 2018. For each request for the Bonferroni procedure a line of data is generated logging the users input. During 2018 18075 requests were made, on average about 50 per day. In a first sweep through the data 1403 requests were removed. This removal included attempts to hack the website, requests generated by the author of this paper and associates, and requests by search engine bots. In a next step 2153 requests were removed which had out of range input values. This way 14519 valid requests remained for analysis, about 40 valid requests per day. User behavior was aggregated into two hour sessions, behavior outside the two hours was considered the next session. Some analysis was done by Internet Protocol (IP) address, however, IP address is a difficult indicator to use for an analysis as it cannot be traced back to a single user or computer. For example, each person logging into a company or university network is given a different IP address out of the organization's stock for each login, a number which has been previously used by others in the same organization.

The analysis of this data was done using 'R' statistical software and excel spreadsheets.

RESULTS

The 14519 valid requests were produced by 5589 IP address within 8460 sessions. Each session contained on average of 1.7 requests for a Bonferroni adjusted p-value. 5724 (67.7%) of the sessions were only one request long, 2474 (29.4%) between two and five, and 262 (3.1%) had more than five requests. An analysis by IP address gives a similar result, most users did very few requests, however, there were some heavy users, 3 IP address did more than 70 requests at different times and days.

Table 1. Adjusted and Unadjusted Alpha and Correlation Used in the Bonferroni Procedure

Table one shows in the second column the frequency distribution of the p-values given by the users to the program. The value 0.05 is given by 84.1% of the users; 9.5% of the users give a value less than 0.05; 6.4% a larger value. Of the users 33% specifies (not in the table) that the number of multiple tests, to which the Bonferroni correction has to apply, is five or less, 42.8% specifies a number between 5 and 11, 17.1% between 10 and 101 and 7.1% sets the number higher than 100. The result of the Bonferroni correction, i.e. the number of tests applied to the alpha values, is in the third column of table one. Of the users 67.9% ends up with a Bonferroni adjusted p-value of less than 0.01, 31.0% with a p-value between 0.01 and 0.05, 2.1% with a p-value more than 0.05.

The default of the correlation program is a correlation of zero, so no consideration of a correlation between multiple tests. Of the 14519 requests 2947 or 20.2% specified a correlation higher than zero. The frequency distribution of these correlations is shown in the fourth column of table one. As can be seen in the table, bottom line, 45% of requests specifies a correlation similar or larger than 0.5. In the last column the frequency distribution of Bonferroni corrected p-values considering correlation is given. Particularly interesting is to compare this column with the third column, correction without correlation adjustment. Considering a correlation about halves the cases with a very low p-value (p<0.01), on the first row, as a result of Bonferroni correction.

Holm's step wise method is another way to address the low power of Bonferroni correction. Of the 14519 requests 1790 (14.1%) included a request for Holm's correction.

CONCLUSION

There is no logical reason why an error type one, incorrectly rejecting the H0 and running the risk of introducing ineffective interventions, should be considered as more serious compared with an error type two, incorrectly accepting the H0 and not introducing effective interventions. Bonferroni correction lowers the power of statistical tests and raises the risk a heightened error type two. This should be of utmost concern when Bonferroni correction is applied. The way the users used the Bonferroni correction on the website, particularly the high number of multiple tests considered, often led to a very conservative result.

Website trace data shows only part of a picture. And in the case of the data discussed here it is impossible to know what the motivation and aim of the visitors to use the procedure has been. Many will have come by chance, browsing the internet, maybe spurred on by suggestions of a search website and links found on other sites. They might have tapped in some numbers, seen the results, and moved on without much thought and without intent to apply the results and the lessons learnt. It is hard to know how often this happened; however, what pleads against the scenario of much random behavior is the fact that the input was mostly valid. Where proportions were expected proportions were given, and were integer numbers were expected integer numbers were given. A small proportion of unrealistically high p-values was given but these might have been user errors.

There are a number of studies which show the use of Bonferroni correction in published papers (2,19). That is the reality of the use of Bonferroni correction in the context of a successful publication. This paper shows more the dynamics of searching for the Bonferroni correction method before a publication. The first thing to note is that there isn'st much searching going on. Mostly only one request for a Bonferroni correction was made. Why only one so often? Maybe the user was just testing the procedure before moving on. Maybe the user had the situation all clear-cut and was just looking for the calculation to be done. Which leaves the question, why is only one Bonferroni correction done, why not more? To use more than one multiplicity correction in a study is rarely suggested, however, such a strategy might solve some of the problems associated with low power in Bonferroni correction (8). Bonferroni correction should be question and not study based and a study would normally consist of more than a single question.

Although there is critique on a p-value of 0.05 (20-22) on the website it is most often used. The few users which preferred a different value mostly wanted a smaller value. The number of multiple tests to consider was often large. The advice is to limit the number of outcomes in a study (23,24). The result of the large numbers of multiple tests specified by the users is that the p-value which results after Bonferroni correction is small. There were a few cases which requested a very large number of multiple tests. It should be noted in this context that in some laboratory and biology studies very large numbers of tests are done on a single hypothesis (25,26).

Only 20.2% of requests specified a correlation. However, the correlation given is mostly high, about 45% of users requested a correlation above 0.5. In these cases considering the correlation has a very significant effect on the Bonferroni correction. The 68% of p-values below 0.01 was almost halved.

Holm's method is another way to address the low power which results when Bonferroni correction is applied. About 14% of requests asked for the Holm's method. This seems to be a very low percentage given the advice that this method should be more often used (14).

Recommendations.

For the readers who, after careful consideration, decide to apply Bonferroni correction the following recommendations seem relevant: 1) what constitutes a family of tests should be carefully considered and defining more than a single family should become more usual; 2) if there is no good reason to change keep the starting p-value at 0.05; 3) except for rare cases the number of outcomes or groups should be limited to only a few; 4) in the case of multiple outcomes particularly always use correlation correction; 5) prefer the Holm's correction, mostly there is no reason to prefer the very conservative Bonferroni correction.

The data used for this paper can be found here.