Simple Interactive Statistical Analysis
Bonferroni
Input.
Input should be the pursued alpha level, a decimal number between 'zero' and 'one' in the top box. The number of comparisons, a positive integer number without decimals, is given in the second box.
Optional, one can set the mean r (correlation) to zero for full Bonferoni correction and to a value between 0 and 1 for partial Bonferroni correction.
A further option is to give the degrees of freedom to obtain the critical value for t, instead of the critical value for z. The degrees of freedom should be the number of cases in the study minus one. Also, if degrees of freedom are given the t-value is given for the comparison of k>2 independent means, according to Scheffé's method. The degrees of freedom in this case should also be the number of cases minus one.
The Holm method is a top-down stepwise procedure whereby the Bonferroni procedure is recalculated time after time for the hypothesis left to test. Comparing observed p-values with critical p-values step by step, as soon as a non-significant p-value is found all remaining p-values are declared non-significant. This cryptic description is illustrated in the table.
| order | Holm-B | Holm-S | B-H | your-p | Holm | B-H |
| 1 | 0.00714286 | 0.00730083 | 0.00714286 | 0.00001 | smallest | smallest |
| 2 | 0.00833333 | 0.00851244 | 0.01428571 | 0.00099 | ↓ | ↑ |
| 3 | 0.01 | 0.01020622 | 0.02142857 | 0.003 | ↓ | ↑ |
| 4 | 0.0125 | 0.01274146 | 0.02857143 | 0.0145 | ↓ | ↑ |
| 5 | 0.01666667 | 0.01695243 | 0.03571429 | 0.016 | ↓ | ↑ |
| 6 | 0.025 | 0.02532057 | 0.04285714 | 0.06 | ↓ | ↑ |
| 7 | 0.05 | 0.05 | 0.05 | 0.13 | largest | largest |
For the Holm method you order your p-values from smallest to largest in the "your p" column. According to the Holm procedure you start in the first row, in this row your-p is smaller than the critical p, the p-value is declared statistically significant. Continue doing this until you reach the 4th row. In this row your-p is larger than the critical p. Declare this p and all p-values larger than this p non-significant, including the p-value in the fifth row, which is lower than the critical p-value. Holm-B is based on the Bonferroni procedure, Holm-S on the Sidak procedure.
Bonferroni adjustment procedures (generally named "family-wise error rate (FWER)" procedures) are correct if you want to control the occurrence of a single false positive, one or more incorrectly significant declared results, in a family of N tests. False discovery rate (FDR) procedures are based on the notion of having a prior expected proportion of false positives among k significant declared tests. If the p-values are from independent tests the binomial cumulative function gives you the FEWR given a certain FDR. Say, you expect 5% of 10 positive outcomes to be false positive, then there is a 40% probability of one or more false positives, an 8.6% probability of two or more false positives, etc. $
One such FDR procedure is the Benjamini-Hoghberg procedure. The p in the alpha box now stands for proportion, and no longer for probability. It is the proportion of false positive results in the statistically significant results. This proportion is sometimes set higher as the usual 0.05, dependent of the cost-benefit of a particular outcome (McDonald, 2009). However, this would increase the number of false positives. In the Benjamini-Hochberg procedure you work bottom-up. The p-value in the 7th row is larger than the critical p-value and declared non-significant. Same for the 6th row. However, in the 5th row your-p is smaller than the critical p-value. You stop testing and declare this p-value and all p-values smaller than this p-value statistically significant. This test requires the p-values to be independent. Thus, the test is valid if you compare the p-value of the comparison A<->B with the p-value of the comparison C<->D. However, the test is mostly not valid in comparing the p-value A<->B with the p-value A<->C. If A is larger than B it is more likely to be also larger than C.
Benjamini and Yukutieli proposed the divisor "c" in case the assumptions of the B-H procedure are not met. In the case of independence or positive correlation of the tests c=1. So nothing changes. In the case of arbitrary or unknown dependence you need to divide the B-H critical values by the Benjamini-Yukutieli divisor in the output. The step-up method further works the same. In the case of the table above the Benjamini-Yukutieli divisor=2.593 and the critical values then become 0.00714/2.593=0.0028; 0.0142/2.593=0.0055; 0.0083; 0.011; 0.0138; 0.0165 and 0.0193 respectively. With Benjamini and Yukutieli correction only the p-values in the first three rows are declared statistically significant.
Choices.
The best choice in any case would be the Holm-Sidak. Note that the correlation adjusted methods are less well researched and not generally accepted. Further, consider that in many cases the best choice is not to use any of these procedures and to leave the p-values uncorrected. The Benjamini-Hoghberg is a conceptually unusual procedure only to be applied to answer the specific question of the false discovery rate.
Rules.
There are a number of good overviews which discuss when (not) to apply Bonferroni adjustment, in particular the overview by Bender & Lange (2001) is helpful. However, a number of rules might be followed. If you have one question or hypothesis at the beginning and a single answer or conclusion at the end, and more than one look at the data or multiple statistical tests in between, Bonferroni adjustment should very seriously be considered. If besides your one question and conclusion you have some new observations and questions at the end, then the statistics or observations which generated the new questions should certainly not be Bonferroni corrected. The new observations will have to be confirmed on a separate dataset. More complex, if you have a vague and general question at the beginning and a number of conclusions and new questions at the end, with a couple of looks at the data in between, then Bonferroni adjustment is probably not appropriate. But maybe it is.
Correlated comparisons.
There are two quite general situations in research, multiple groups and multiple outcomes. A multiple group situation is for example when there is a group which receives no treatment, compared with a group on current treatment, compared with group new treatment A compared with group new treatment B. Anova is the most often used method of analysis in this case. Note, the Anova itself will never be Bonferroni corrected but the multiple comparisons which follow will be. If the conclusion would be that there is an effect if there is a statistically significant difference between any combination of two groups, then the analysis has to be Bonferroni corrected, with ~criticalP/6. (=n(n-1)/2=4(4-1)/2=6)
Multiple group tests assume independence but rarely are groups independent with regard to an outcome variable . Say treatment A and treatment B are different doses of the same active ingredient, then there is probably dependence between the groups with regard to the outcome of the study. If there is statistical significance between current treatment and treatment A, there is a much increased probability that there is also statistical significance between current treatment and treatment B. The Bonferroni adjustment then would have to be ~criticalP/(6*correction factor) whereby 0<correction factor<1. If treatment group A and treatment group B would get the same treatment these two groups would have to be collapsed into one and the number of comparisons above would be 3 instead of 6. However, it is very hard to know retrospectively if two groups got about the same treatment, as different groups behave very much like different groups regardless of the treatment provided.
The square root of the explained variance in ANOVA gives an indication of the dependence or correlation between multiple groups with regard to an outcome. SISA's t-test procedure gives an estimate of the correlation between two groups.
Multiple outcomes is when more than one outcome is measured on each study subject, for example for each person in the study we observe 1) dizziness, 2) depression, 3) fatigue and 4) headaches. The treatment is concluded to be effective if there is an effect in one of these outcomes. Clear case of Bonferroni adjustment required. Full Bonferroni adjustment can be used if there is no dependence between the outcome variables. Thus, the treatment has an effect on headaches, but might or might not have an effect on any of the other outcomes. No Bonferroni adjustment should be applied if the outcomes are totally dependent. If the treatment has an effect on dizziness it will have a similarly powerful effect on any of the other outcomes. Basically, the above mentioned medical problems are just different names for one medical phenomenon.
In practice in any design there will always be some dependence and the appropriate Bonferroni adjustment will be on a curve between no correction and full correction. This is illustrated in the figure:
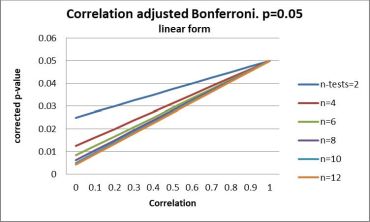
The top right corner of the figure, where all the lines come together, shows the example of no Bonferroni adjustment. Full Bonferroni adjustment can be seen on the left, were the distance between the lines is largest. Given the example of the above mentioned four medical problems, the average in a triangular matrix of the six correlations between the outcome measures could be 0.3. We do four comparisons between the experimental and the control group, then the critical value for each comparison should be according to the red line in the figure about 0.025. Adjustment according to this figure is given in the webpage if you give a correlation and check the box.

In the SISA correlated Bonferroni program the default is the D/AP procedure as discussed by Sankoh et.al. (1997). The results for the D/AP method are shown in the second figure. What the figure shows is that the D/AP procedure is relatively conservative and has a tendency towards the full Bonferroni adjustment in the case of moderate correlation between outcome variables, particularly when the number of comparisons is large. When the correlation equals 0.5 the correlation adjusted D/AP-Sidak is equivalent to the Tukey, Chiminera and Heyse (THC) Adjustment (1985).
Bender R, & Lange S. Adjusting for multiple testing—when and how?. Journal of clinical epidemiology 2001;54.4:343-349.
McDonald JH. Multiple comparisons. In: McDonald, John H. Handbook of biological statistics. Vol. 2. Baltimore, MD: Sparky House Publishing, 2009.
Perneger TV. What is wrong with Bonferroni adjustments. British Medical Journal 1998;136:1236-1238.
Rothman KJ. No adjustments are needed for multiple comparisons. Epidemiology 1990;1.1:43-46.
Sankoh AJ, Huque MF, & Dubey SD. Some comments on frequently used multiple endpoint adjustments methods in clinical trials. Statistics in Medicine 1997;16:2529-2542.
Tukey, JW, Ciminera JL, & Heyse JF. Testing the statistical certainty of a response to increasing doses of a drug. Biometrics 1985:295-301.
Quantitativeskills. Use of Bonferroni Multiple Testing Correction With an Internet Based Calculator. An Analysis of User Behaviour. Hilversum (NL): Internal Publication, 2019.
$: When proportion FDR of N positively tested independent results is expected to be false then the probability of at least one false positive result FWER=1-(1-FDR)N; FDR=1-(1-FWER)1/N
